C++ Tutorial
- Binary Tree Code Example
I think that I shall never see
A graph more lovely than a tree.
A tree whose crucial property
Is loop-free connectivity.
A tree that must be sure to span
So packets can reach every LAN.
First, the root must be selected.
By ID, it is elected.
Least-cost paths from root are traced.
In the tree, these paths are placed.
A mesh is made by folks like me,
Then bridges find a spanning tree.
- Radia Perlman (Developer of Spanning Tree)
A binary tree is made of nodes, where each node contains a left pointer, a right pointer, and a data element.
The root pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller subtrees on either side. A null pointer represents a binary tree with no elements -- the empty tree.
The formal recursive definition is: a binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.
A binary search tree (BST) or ordered binary tree is a type of binary tree where the nodes are arranged in order: for each node, all elements in its left subtree are less-or-equal to the node (<=), and all the elements in its right subtree are greater than the node (>).
Basically, binary search trees are fast at insert and lookup. On average, a binary search tree algorithm can locate a node in an $n$ node tree in order $ \log n$ time (log base 2). Therefore, binary search trees are good for dictionary problems where the code inserts and looks up information indexed by some key. The $ \log n$ behavior is the average case -- it's possible for a particular tree to be much slower depending on its shape.
The last tree out of major kinds of trees is a heap. A heap is a tree in which each node's children have values less than or equal to node's value. Consequently, the root node always has the largest value in the tree, which means that it's possible to find the maximum value in constant time: Simply return the root value. So, if extraction the max value needs to be fast, we should use a heap.
A leaf (external) node is a node that has no children while nonleaf node is also called internal node. The number of children of a node $x$ in a tree $T$ is the same as the degree of $x$. The length of the simple path from the root $r$ to a node $x$ is the depth of $x$ in $T$. A level of a tree consists of all nodes at the same depth. The height of a node in a tree is the number of edges (hops) on the longest downward path from the node to a leaf, and the height of a tree is the height of its root. So, the height of a tree is equal to the largest depth of any node in the tree.
The height (depth) could be anywhere from ~$log_2 n$(best case, perfectly balanced) to ~$n$ (worst case, a chain). Another thing to point out here is the importance of the height. We may appreciate the role of the height property of BST from the answer to the following question:
What's the worst-case running time of search(or insert) operation in a binary search tree containing $n$ keys?
- $O(1)$
- $O(log_2 n)$
- $O(height)$
- $O(n)$
- Look Up (lookUp())
One advantage of a binary search tree is that the lookup operation is fast and simple. This is particularly useful for data storage. This look up is a fast operation because we eliminate half the nodes from our search on each iteration by choosing to follow the left subtree or the right subtree. It is an $ \Omega (\log n)$ operation. - New Node (newTreeNode())
Makes the root node. - Insert Node (insertTreeNode())
Insertion begins as a search would begin; if the root is not equal to the value, we search the left or right subtrees as before. Eventually, we will reach an external node and add the value as its right or left child, depending on the node's value. In other words, we examine the root and recursively insert the new node to the left subtree if the new value is less than the root, or the right subtree if the new value is greater than or equal to the root.
$ \Omega (\log n)$ operations - Deleting a key from a binary search ( deleteKey())
This is a little bit tricky. We can categorize it in three groups depending its operations:- A leaf node - this is the easiest case and we just delete it.
- A node that has both left and right child
We replace the node with its predecessor. - A node that has only one child. The child replaces the parent.
- Is The Given Tree BST? (isBST())
The code isBST() is the answer to the question:
Given a binary tree, programmatically we need to prove it is a binary search tree.
If the given binary tree is a binary search tree, then the inorder traversal should output the elements in increasing order.
We make use of this property of inorder traversal to check whether the given binary tree is a BST or not. - Size (treeSize())
Size of a binary tree is the total number of nodes in the tree. - Maximum/Minimum Depth (maxDepth()/minDepth())
The number of nodes along the longest/shortest path from the root node down to the farthest leaf node. The maxDepth of the empty tree is 0. - Is balanced? (isBalanced())
A balanced binary tree is commonly defined as a binary tree in which the height of the two subtrees of every node never differ by more than 1.
In this example, I used maxDepth(node)-minDepth(node) <= 1 - Minimum/Maximum Value (minTree()/maxTree())
- In Order Successor/Predecessor (succesorInOrder()/predecessorInOrder())
A node which has the next higher/lower key.
- Successor
A node's successor is the one with the next largest value in the tree. In other words, if all keys are distinct, the successor of a node $x$ is the node with the smallest key greater than $x.key$. The structure of binary search tree allows us to determine the successor of a node without ever comparing the keys.
For example, given the tree in the picture above, the successor of B is C, the successor of E is F, and the successor of I is None. Finding the successor involves two distinct cases.
(a) If a node has a right child, then the successor is the minimum of the minor tree. For example, to find the successor of B, we know it has a right hand child, D, so we take its minimum, C.
(b) If a node has no right child, as in the case with E, we need to search back up the tree until we find the first right-hand turn. In other words, we keep looking up the tree until we find a node that is the left child, and then use its parent. In our example, we move up the tree moving left from E to D, and then left again to B, and finally we make a right-hand turn to F.
The following pseudo code returns the successor of a node $x$ in a binary search tree if it exists, or NULL if $x$ has the largest key in the tree:SuccessorInOrder(x) if x.right != NULL; return minTree(x); y = x.p while x!= NULL && x == y.right x = y; y = x.p; return y;As described earlier, we broke the code into two cases. If the right subtree of node $x$ is not empty, then the successor of $x$ is just the leftmost node in $x$'s right subtree. So, we just call minTree(x). However, if the right subtree of node $x$ is empty, to find $y$, we simply go up the tree from $x$ until we see a node that is the left child of its parent. - Predecessor
For example, given the tree in the picture above, the predecessor of B is A, the predecessor of E is D, and the predecessor of I is H.
The algorithm for finding the predecessor is , in essence, the inverse of what we use for the successor, and it also involves two similar cases.
(a) If a node has a left child, then we take subtree's maximum, i.e. right-most child of its left subtree.
(b) If a node has no left child, we walk up the tree until we find a left-hand turn. In other words, follow the parent pointer until we get the key which is smaller than its own value.
- Successor
- LCA (Lowest Common Ancestor) - (lowestCommonAncestor())
For the picture above,
The lowest common ancestor of A and C is B
The lowest common ancestor of E and H is F
The lowest common ancestor of D and E is B
The lowest common ancestor of G and I is F
The lowest common ancestor of H and I is G
- Clear (Delete Node)
$ \Omega (\log n)$ operations - In Order print (printTreeInOrder())
As the name suggests, it prints the values in a binary search tree in sorted order.
Inorder traversal performs the operation first on the node's left descendants, then on the node itself, and finally on its right descendants. In other words, the left subtree is visited first, then the node itself, and then the node's right subtree.
If $x$ is the root of an $n$-node subtree, then the call printTreeInOrder(x) takes $\Theta (n)$ time In fact, it prints out exactly one node per one recursive call.
if x != NULL printTreeInOrder(x.left); print x.key; printTreeInOrder(x.right);Also called Inorder tree walk. - Pre Order print (printTreePreOrder())
Preorder traversal involves walking around the tree in a counterclockwise manner starting at the root. It first visits the root node, then each of the subtree.
Sticking close to the edge, and printing out the nodes as we encounter them. For the tree shown above, the result is F B A D C E G I H.
Traversal operation performed first on the node itself, then on its left descendants, and finally on its right descendants. In other words, a node is always visited before any of its children.
Also called Preorder tree walk. - Post Oder print (printTreePostOrder())
Postorder traversal performs the operation first on the node's left descendants, then on the node's right descendants, and finally on the node itself. In other words, all of a node's children are visited before the node itself.
For the picture above, it will be - A C E D B H I G F.
Also called Postorder tree walk. - Reverse Oder print (printTreeReverseOrder())
Reversing the traverse of the printTreeInOrder().
This will print - I H G F E D C B A. - Converting Binary Search Tree into an Array (TreeToArray())
How do you put a Binary Search Tree in an array in an efficient manner.
Hint :: If the node is stored at the ith position and its children are at 2i and 2i+1(I mean level order wise). It's not the most efficient way. - Paths from the root to leaves (pathFinder())
Given a binary tree, print out all of its root-to-leaf paths, one per line. Uses a recursive helper to do the work. - Find n-th maximum node (NthMax())
How do we find out the fifth maximum element in a Binary Search Tree in efficient manner?
Note: We should not use any extra space. i.e., sorting Binary Search Tree and storing the results in an array and listing out the fifth element. - Is Sub Tree? (isSubTree())
- Mirror Tree (mirror())
Change a tree so that the roles of the left and right hand pointers are swapped at every node. - Make a new tree with minimal depth from a sorted array (createMinimalBST(())
- Get the level for a given node element (getLevel(root, elm, 0))
- Separate elements depending on the level (even/odd) (level_even_odd(root);)
This function utilizes BFS, and can be used to calculate the sum of element at even levels or odd levels.
For example, given a binary tree. Write a function that takes only root node as argument and returns (sum of values at odd height)-(sum of values at even height). - Traversing level-order: Breadth-first traversal
It's nice when we have a tree with ordering properties such as a BST or a heap. Often we're given a tree that isn't BST or a heap. For instance, we may have a tree that is a representation of a family tree or a company job hierarchy. We have to use different techniques to retrieve data from this kind of tree. One common class of problems involves searching for a particular node. There are two very common search algorithms.
One way to search a tree is to do a breadth-first search (BFS). In a BFS we start with the root, move left to right across the second level, then move left to right across the third level, and so on. We continue the search until either we have examined all of the nodes or we find the node we are searching for. The time to find a node is O(n), so this type of search is best avoided for large trees. A BFS also uses a large amount of memory because it is necessary to track the child nodes for all nodes on a given level while searching that level.
BreadthFirstTraversal()
- Printing elements at the same level
- BreadthFirst_LevelElement_Print(root, levVec)
It is used to print all elements at the same level (depth). The parameters are root and 2D vector levVec. The vector has the depth information and being used to set the size of the first index which is index for level. While traversing with Breadth First approach, each node will be pushed into the vector after finding the level of the element using getLevel() function. So, it looks like this for the tree diagram above.Level at 0: F Level at 1: B G Level at 2: A D I Level at 3: C E H - levelPrint(root, elm, level)
Prints all nodes at the same level.
This is simpler than BreadthFirst_LevelElement_Print().
It takes 2D vector (elm) with the same size of level (= MaxDepth+1) and fills elements as we traverse (preOrder).
- BreadthFirst_LevelElement_Print(root, levVec)
- Depth-First Search
Another common way to search for a node is by using a depth-first search (DFS). A depth-first search follows one branch of the tree down as many levels as possible until the target node is found or the end is reached. When the search can't go down any farther, it is continued at the nearest ancestor with unexplored children. DFS has much lower memory requirements than BFS because it is not necessary to store all of the child pointers at each level. In addition, DFS has the advantage that it doesn't examine any single level last (BFS examines the lower level last). This is useful if we suspect that the node we are searching for will be in the lower levels. In this case, a DFS would usually find the target node more quickly than a BFS.
InOrder(), PreOrder(), PostOrder() - Check if the roots are equal or both NULL
- Check if one of them is NULL
- Check node, left subtree, and then right subtree
- A leaf node - this is the easiest case and we just delete it.
- A node that has both left and right child
We replace the node with its predecessor. - A node that has only one child. The child replaces the parent.
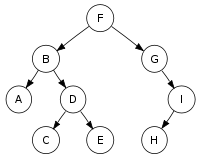
The following items are included in this Binary Search Tree example code.
It's based on the tree in the picture above.
Here is the file for Binary Tree example below: BinaryTree.cpp.
/* Binary Tree */
#include <iostream>
#include <deque>
#include <climits>
#include <vector>
using namespace std;
struct Tree
{
char data;
Tree *left;
Tree *right;
Tree *parent;
};
Tree* lookUp(struct Tree *node, char key)
{
if(node == NULL) return node;
if(node->data == key) return node;
else {
if(node->data < key)
return lookUp(node->right, key) ;
else
return lookUp(node->left, key);
}
}
Tree* leftMost(struct Tree *node)
{
if(node == NULL) return NULL;
while(node->left != NULL)
node = node->left;
return node;
}
struct Tree *newTreeNode(int data)
{
Tree *node = new Tree;
node->data = data;
node->left = NULL;
node->right = NULL;
node->parent = NULL;
return node;
}
struct Tree* insertTreeNode(struct Tree *node, int data)
{
static Tree *p;
Tree *retNode;
//if(node != NULL) p = node;
if(node == NULL) {
retNode = newTreeNode(data);
retNode->parent = p;
return retNode;
}
if(data <= node->data ) {
p = node;
node->left = insertTreeNode(node->left,data);
}
else {
p = node;
node->right = insertTreeNode(node->right,data);
}
return node;
}
void isBST(struct Tree *node)
{
static int lastData = INT_MIN;
if(node == NULL) return;
isBST(node->left);
/* check if the given tree is BST */
if(lastData < node->data)
lastData = node->data;
else {
cout << "Not a BST" << endl;
return;
}
isBST(node->right);
return;
}
int treeSize(struct Tree *node)
{
if(node == NULL) return 0;
else
return treeSize(node->left) + 1 + treeSize(node->right);
}
int maxDepth(struct Tree *node)
{
if(node == NULL || (node->left == NULL && node->right == NULL))
return 0;
int leftDepth = maxDepth(node->left);
int rightDepth = maxDepth(node->right);
return leftDepth > rightDepth ?
leftDepth + 1 : rightDepth + 1;
}
int minDepth(struct Tree *node)
{
if(node == NULL || (node->left == NULL && node->right == NULL))
return 0;
int leftDepth = minDepth(node->left);
int rightDepth = minDepth(node->right);
return leftDepth < rightDepth ?
leftDepth + 1 : rightDepth + 1;
}
bool isBalanced(struct Tree *node)
{
if(maxDepth(node)-minDepth(node) <= 1)
return true;
else
return false;
}
/* Tree Minimum */
Tree* minTree(struct Tree *node)
{
if(node == NULL) return NULL;
while(node->left)
node = node -> left;
return node;
}
/* Tree Maximum */
Tree* maxTree(struct Tree *node)
{
while(node->right)
node = node -> right;
return node;
}
/* In Order Successor - a node which has the next higher key */
Tree *succesorInOrder(struct Tree *node)
{
/* if the node has right child, seccessor is Tree-Minimum */
if(node->right != NULL) return minTree(node->right);
Tree *y = node->parent;
while(y != NULL && node == y->right) {
node = y;
y = y->parent;
}
return y;
}
/* In Order Predecessor - a node which has the next lower key */
Tree *predecessorInOrder(struct Tree *node)
{
/* if the node has left child, predecessor is Tree-Maximum */
if(node->left != NULL) return maxTree(node->left);
Tree *y = node->parent;
/* if it does not have a left child,
predecessor is its first left ancestor */
while(y != NULL && node == y->left) {
node = y;
y = y->parent;
}
return y;
}
void reverseOrderPrint(struct Tree *node)
{
if(node == NULL) return;
if(node->left == NULL && node->right == NULL) {
cout << node->data << " ";
return;
}
reverseOrderPrint(node->right);
cout << node->data << " ";
reverseOrderPrint(node->left);
}
Tree *lowestCommonAncestor(Tree *node, Tree *p, Tree *q)
{
Tree *left, *right;
if(node == NULL) return NULL;
if(node->left == p || node->left == q
|| node->right == p || node->right == q) return node;
left = lowestCommonAncestor(node->left,p,q);
right = lowestCommonAncestor(node->right, p,q);
if(left && right)
return node;
else
return (left) ? left : right;
}
void clear(struct Tree *node)
{
if(node != NULL) {
clear(node->left);
clear(node->right);
delete node;
}
}
/* print tree in order */
/* 1. Traverse the left subtree.
2. Visit the root.
3. Traverse the right subtree.
*/
void printTreeInOrder(struct Tree *node)
{
if(node == NULL) return;
printTreeInOrder(node->left);
cout << node->data << " ";
printTreeInOrder(node->right);
}
/* print tree in postorder*/
/* 1. Traverse the left subtree.
2. Traverse the right subtree.
3. Visit the root.
*/
void printTreePostOrder(struct Tree *node)
{
if(node == NULL) return;
printTreePostOrder(node->left);
printTreePostOrder(node->right);
cout << node->data << " ";
}
/* print in preorder */
/* 1. Visit the root.
2. Traverse the left subtree.
3. Traverse the right subtree.
*/
void printTreePreOrder(struct Tree *node)
{
if(node == NULL) return;
cout << node->data << " ";
printTreePreOrder(node->left);
printTreePreOrder(node->right);
}
/* In reverse of printTreeInOrder() */
void printTreeReverseOrder(struct Tree *node)
{
if(node == NULL) return;
if(node->left == NULL && node->right == NULL) {
cout << node->data << " ";
return;
}
printTreeReverseOrder(node->right);
cout << node->data << " ";
printTreeReverseOrder(node->left);
}
/* recursion routine to find path */
void pathFinder(struct Tree *node, int path[], int level)
{
if(node == NULL) return;
// save leaf node
if(node->left == NULL && node->right == NULL) {
path[level] = node->data;
for(int i = 0; i <= level; i++) {
cout << (char)path[i];
}
cout << endl;
return;
}
// save parent node
path[level] = node->data;
pathFinder(node->left, path, level+1);
pathFinder(node->right, path, level+1);
}
bool matchTree(Tree *r1, Tree *r2)
{
/* Nothing left in the subtree */
if(r1 == NULL && r2 == NULL)
return true;
/* Big tree empty and subtree not found */
if(r1 == NULL || r2 == NULL)
return false;
/* Not matching */
if(r1->data != r2->data)
return false;
return (matchTree(r1->left, r2->left) &&
matchTree(r1->right, r2->right));
}
bool subTree(Tree *r1, Tree *r2)
{
/*Big tree empty and subtree not found */
if(r1 == NULL)
return false;
if(r1->data == r2->data)
if(matchTree(r1, r2)) return true;
return
(subTree(r1->left, r2) || subTree(r1->right, r2));
}
bool isSubTree(Tree *r1, Tree *r2)
{
/* Empty tree is subtree */
if(r2 == NULL)
return true;
else
return subTree(r1, r2);
}
/* change a tree so that the roles of the left
and right hand pointers are swapped at every node */
void mirror(Tree *r)
{
if(r == NULL) return;
Tree *tmp;
mirror(r->left);
mirror(r->right);
/* swap pointers */
tmp = r->right;
r->right = r->left;
r->left = tmp;
}
/* create a new tree from a sorted array */
Tree *addToBST(char arr[], int start, int end)
{
if(end < start) return NULL;
int mid = (start + end)/2;
Tree *r = new Tree;
r->data = arr[mid];
r->left = addToBST(arr, start, mid-1);
r->right = addToBST(arr, mid+1, end);
return r;
}
Tree *createMinimalBST(char arr[], int size)
{
return addToBST(arr,0,size-1);
}
/* Breadth first traversal using queue */
void BreadthFirstTraversal(Tree *root)
{
if (root == NULL) return;
deque <Tree *> queue;
queue.push_back(root);
while (!queue.empty()) {
Tree *p = queue.front();
cout << p->data << " ";
queue.pop_front();
if (p->left != NULL)
queue.push_back(p->left);
if (p->right != NULL)
queue.push_back(p->right);
}
cout << endl;
}
/* get the level of a node element: root level = 0 */
int getLevel(struct Tree *node, int elm, int level)
{
if(node == NULL) return 0;
if(elm == node->data)
return level;
else if(elm < node->data)
return getLevel(node->left, elm, level+1);
else
return getLevel(node->right, elm, level+1);
}
/* This code prints out all nodes at the same depth (level) */
void BreadthFirst_LevelElement_Print
(struct Tree *root, vector<vector<int> > &v;)
{
if(root == NULL) return;
deque<Tree *> q;
q.push_back(root);
while(!q.empty()) {
Tree *p = q.front();
int lev = getLevel(root, p->data, 0);
v[lev].push_back(p->data);
q.pop_front();
if(p->left) q.push_back(p->left);
if(p->right)q.push_back(p->right);
}
return;
}
/* levelPrint()
prints nodes at the same level
This is simpler than the BreadthFirstTraversal(root) above
It takes 2D vector with the same size of level (= MaxDepth+1)
and fills elements as we traverse (preOrder) */
void levelPrint(struct Tree *node, vector<vector<char> >&elm;, int level)
{
if(node == NULL) return;
// leaf nodes
if(node->left == NULL && node->right == NULL) {
elm[level].push_back(node->data);
return;
}
// other nodes
elm[level++].push_back(node->data);
levelPrint(node->left, elm, level);
levelPrint(node->right, elm, level);
}
/* find n-th max node from a tree */
void NthMax(struct Tree* t)
{
static int n_th_max = 5;
static int num = 0;
if(t == NULL) return;
NthMax(t->right);
num++;
if(num == n_th_max)
cout << n_th_max << "-th maximum data is "
<< t->data << endl;
NthMax(t->left);
}
/* Converting a BST into an Array */
void TreeToArray(struct Tree *node, int a[]){
static int pos = 0;
if(node){
TreeToArray(node->left,a);
a[pos++] = node->data;
TreeToArray(node->right,a);
}
}
/* Separate even/odd level elements */
/* This function is using BFS */
void level_even_odd(struct Tree *node)
{
vector<char> evenVec, oddVec;
if (node == NULL) return;
deque<struct Tree*> que;
que.push_back(node);
while(!que.empty())
{
struct Tree *p = que.front();
int level = getLevel(node, p->data, 0) ;
// even level
if (level % 2 == 0)
evenVec.push_back(p->data);
else
oddVec.push_back(p->data);
que.pop_front();
if(p->left) que.push_back(p->left);
if(p->right) que.push_back(p->right);
}
cout << "even level elements : ";
for(int i = 0; i < evenVec.size(); i++)
cout << evenVec[i] << " ";
cout << endl << "odd level elements : ";
for(int i = 0; i < oddVec.size(); i++)
cout << oddVec[i] << " ";
cout << endl;
}
int main(int argc, char **argv)
{
char ch, ch1, ch2;
Tree *found;
Tree *succ;
Tree *pred;
Tree *ancestor;
char charArr[9]
= {'A','B','C','D','E','F','G','H','I'};
Tree *root = newTreeNode('F');
insertTreeNode(root,'B');
insertTreeNode(root,'A');
insertTreeNode(root,'D');
insertTreeNode(root,'C');
insertTreeNode(root,'E');
insertTreeNode(root,'G');
insertTreeNode(root,'I');
insertTreeNode(root,'H');
/* is the tree BST? */
isBST(root);
/* size of tree */
cout << "size = " << treeSize(root) << endl;
/* max depth */
cout << "max depth = " << maxDepth(root) << endl;
/* min depth */
cout << "min depth = " << minDepth(root) << endl;
/* balanced tree? */
if(isBalanced(root))
cout << "This tree is balanced!\n";
else
cout << "This tree is not balanced!\n";
/* min value of the tree*/
if(root)
cout << "Min value = " << minTree(root)->data << endl;
/* max value of the tree*/
if(root)
cout << "Max value = " << maxTree(root)->data << endl;
/* get the level of a data: root level = 0 */
cout << "Node B is at level: " << getLevel(root, 'B', 0) << endl;
cout << "Node H is at level: " << getLevel(root, 'H', 0) << endl;
cout << "Node F is at level: " << getLevel(root, 'F', 0) << endl;
/* separate even/odd level elements */
level_even_odd(root);
ch = 'B';
found = lookUp(root,ch);
if(found) {
cout << "Min value of subtree " << ch << " as a root is "
<< minTree(found)->data << endl;
cout << "Max value of subtree " << ch << " as a root is "
<< maxTree(found)->data << endl;
}
ch = 'B';
found = lookUp(root,ch);
if(found) {
succ = succesorInOrder(found);
if(succ)
cout << "In Order Successor of " << ch << " is "
<< succesorInOrder(found)->data << endl;
else
cout << "In Order Successor of " << ch << " is None\n";
}
ch = 'E';
found = lookUp(root,ch);
if(found) {
succ = succesorInOrder(found);
if(succ)
cout << "In Order Successor of " << ch << " is "
<< succesorInOrder(found)->data << endl;
else
cout << "In Order Successor of " << ch << " is None\n";
}
ch = 'I';
found = lookUp(root,ch);
if(found) {
succ = succesorInOrder(found);
if(succ)
cout << "In Order Successor of " << ch << " is "
<< succesorInOrder(found)->data << endl;
else
cout << "In Order Successor of " << ch << " is None\n";
}
ch = 'B';
found = lookUp(root,ch);
if(found) {
pred = predecessorInOrder(found);
if(pred)
cout << "In Order Predecessor of " << ch << " is "
<< predecessorInOrder(found)->data << endl;
else
cout << "In Order Predecessor of " << ch << " is None\n";
}
ch = 'E';
found = lookUp(root,ch);
if(found) {
pred = predecessorInOrder(found);
if(pred)
cout << "In Order Predecessor of " << ch << " is "
<< predecessorInOrder(found)->data << endl;
else
cout << "In Order Predecessor of " << ch << " is None\n";
}
ch = 'I';
found = lookUp(root,ch);
if(found) {
pred = predecessorInOrder(found);
if(pred)
cout << "In Order Predecessor of " << ch << " is "
<< predecessorInOrder(found)->data << endl;
else
cout << "In Order Predecessor of " << ch << " is None\n";
}
/* Lowest Common Ancestor */
ch1 = 'A';
ch2 = 'C';
ancestor =
lowestCommonAncestor(root,
lookUp(root,ch1), lookUp(root,ch2));
if(ancestor)
cout << "The lowest common ancestor of " << ch1 << " and "
<< ch2 << " is " << ancestor->data << endl;
ch1 = 'E';
ch2 = 'H';
ancestor =
lowestCommonAncestor(root,
lookUp(root,ch1), lookUp(root,ch2));
if(ancestor)
cout << "The lowest common ancestor of " << ch1 << " and "
<< ch2 << " is " << ancestor->data << endl;
ch1 = 'D';
ch2 = 'E';
ancestor =
lowestCommonAncestor(root,
lookUp(root,ch1), lookUp(root,ch2));
if(ancestor)
cout << "The lowest common ancestor of " << ch1 << " and "
<< ch2 << " is " << ancestor->data << endl;
ch1 = 'G';
ch2 = 'I';
ancestor =
lowestCommonAncestor(root,
lookUp(root,ch1), lookUp(root,ch2));
if(ancestor)
cout << "The lowest common ancestor of " << ch1 << " and "
<< ch2 << " is " << ancestor->data << endl;
ch1 = 'H';
ch2 = 'I';
ancestor =
lowestCommonAncestor(root,
lookUp(root,ch1), lookUp(root,ch2));
if(ancestor)
cout << "The lowest common ancestor of " << ch1 << " and "
<< ch2 << " is " << ancestor->data << endl;
/* print tree in order */
cout << "increasing sort order\n";
printTreeInOrder(root);
cout << endl;
/* print tree in postorder*/
cout << "post order \n";
printTreePostOrder(root);
cout << endl;
/* print tree in preorder*/
cout << "pre order \n";
printTreePreOrder(root);
cout << endl;
/* print tree in reverse order*/
cout << "reverse order \n";
printTreeReverseOrder(root);
cout << endl;
/* lookUp */
ch = 'D';
found = lookUp(root,ch);
if(found)
cout << found->data << " is in the tree\n";
else
cout << ch << " is not in the tree\n";
/* lookUp */
ch = 'M';
found = lookUp(root,ch);
if(found)
cout << found->data << " is in the tree\n";
else
cout << ch << " is not in the tree\n";
/* printing all paths :
Given a binary tree, print out all of its root-to-leaf
paths, one per line. Uses a recursive helper to do the work. */
cout << "printing paths ..." << endl;
int path[10];
pathFinder(root, path, 0);
/* find n-th maximum node */
NthMax(root);
/* Traversing level-order.
We visit every node on a level before going to a lower level.
This is also called Breadth-first traversal.*/
cout << "printing with Breadth-first traversal" << endl;
BreadthFirstTraversal(root);
/* Prints all element at the same depth (level) */
int row = maxDepth(root);
vector<vector<int> > levVec(row+1);
BreadthFirst_LevelElement_Print(root, levVec);
for(int m = 0; m < levVec.size(); m++) {
cout << "Level at " << m << ": ";
for(int n = 0; n < levVec[m].size(); n++)
cout << (char)levVec[m][n] << " ";
cout << endl;
}
/* levelPrint()
prints nodes at the same level
This is simpler than the BreadthFirstTraversal(root) above
It takes 2D vector (elm) with the same size of level (= MaxDepth+1)
and fills elements as we traverse (preOrder) */
vector<vector<char> > elm;
int mxDepth = maxDepth(root);
elm.resize(mxDepth+1);
int level = 0;
levelPrint(root, elm, level);
cout << "levelPrint() " << endl;
for(int i = 0; i <= mxDepth; i++) {
cout << "level " << i << ": " ;
for(int j = 0; j < elm[i].size(); j++)
cout << elm[i][j] << " ";
cout << endl;
}
/* convert the tree into an array */
int treeSz = treeSize(root);
int *array = new int[treeSz];
TreeToArray(root,array);
cout << "New array: ";
for (int i = 0; i < treeSz; i++)
cout << (char)array[i] << ' ';
cout << endl;
delete [] array;
/* subtree */
Tree *root2 = newTreeNode('D');
insertTreeNode(root2,'C');
insertTreeNode(root2,'E');
cout << "1-2 subtree: " << isSubTree(root, root2) << endl;
Tree *root3 = newTreeNode('B');
insertTreeNode(root3,'A');
insertTreeNode(root3,'D');
insertTreeNode(root3,'C');
insertTreeNode(root3,'E');
cout << "1-3 subtree: " << isSubTree(root, root3) << endl;
Tree *root4 = newTreeNode('B');
insertTreeNode(root4,'D');
insertTreeNode(root4,'C');
insertTreeNode(root4,'E');
cout << "1-4 subtree: " << isSubTree(root, root4) << endl;
cout << "2-3 subtree: " << isSubTree(root2, root3) << endl;
cout << "3-2 subtree: " << isSubTree(root3, root2) << endl;
/* swap left and right */
mirror(root);
/* deleting a tree */
clear(root);
/* make a new tree with minimal depth */
Tree *newRoot = createMinimalBST(charArr,9);
return 0;
}
From the run, we get:
size = 9 max depth = 3 min depth = 2 This tree is balanced! Min value = A Max value = I Node B is at level: 1 Node H is at level: 3 Node F is at level: 0 even level elements : F A D I odd level elements : B G C E H Min value of subtree B as a root is A Max value of subtree B as a root is E In Order Successor of B is C In Order Successor of E is F In Order Successor of I is None In Order Predecessor of B is A In Order Predecessor of E is D In Order Predecessor of I is H The lowest common ancestor of A and C is B The lowest common ancestor of E and H is F The lowest common ancestor of D and E is B The lowest common ancestor of G and I is F The lowest common ancestor of H and I is G increasing sort order A B C D E F G H I post order A C E D B H I G F pre order F B A D C E G I H reverse order I H G F E D C B A D is in the tree M is not in the tree printing paths ... FBA FBDC FBDE FGIH 5-th maximum data is E printing with Breadth-first traversal F B G A D I C E H Level at 0: F Level at 1: B G Level at 2: A D I Level at 3: C E H levelPrint() level 0: F level 1: B G level 2: A D I level 3: C E H New array: A B C D E F G H I New array: A B C D E F G H I 1-2 subtree: 1 1-3 subtree: 1 1-4 subtree: 0 2-3 subtree: 0 3-2 subtree: 1
The following example shows binary serach algorithms using iterative and recursive.
We look for an element x in a sorted array. It compares xx or the array range equals to zero.
#include <iostream>
using namespace std;
// iterative
int bsearch(int a[], int sz, int x)
{
int low = 0;
int high = sz -1;
while(low <= high) {
int mid = (low+high)/2;
if(x < a[mid])
high = mid - 1;
else if(x > a[mid])
low = mid + 1;
else
return a[mid];
}
return -1;
}
// recursive
int bsearch_recursive(int a[], int low, int high, int x)
{
if(low > high) return -1;
int mid = (low + high)/2;
if(x < a[mid])
bsearch_recursive(a, low, mid-1, x);
else if(x > a[mid])
bsearch_recursive(a, mid+1, high, x);
else
return a[mid];
}
void print(int n)
{
if(n == -1) {
cout << "not found" << endl;
return;
}
cout << "found" << endl;
}
int main()
{
int a[]={3, 7, 9, 16, 23, 34, 67, 87, 92};
int arraySize = sizeof(a)/sizeof(int);
int result;
result = bsearch(a, arraySize, 7);
print(result);
result = bsearch(a, arraySize, 92);
print(result);
result = bsearch(a, arraySize, 77);
print(result);
result = bsearch_recursive(a, 0, arraySize-1, 7);
print(result);
result = bsearch_recursive(a, 0, arraySize-1, 92);
print(result);
result = bsearch_recursive(a, 0, arraySize-1, 77);
print(result);
return 0;
}
Output:
found found not found found found not found
/* 3
/ \
-1 2
/ \ /
5 7 1
*/
#include <iostream>
using namespace std;
typedef struct Tree
{
int data;
Tree *left;
Tree *right;
} Node;
/* recursion routine to find path */
void pathFinder(Node* node, int path[], int level)
{
if(node == NULL) return;
// leaf node save
if(node->left == NULL && node->right == NULL) {
path[level] = node->data;
int sum = 0;
for(int i = 0; i <= level; i++) {
cout << path[i] << " ";
sum += path[i];
}
cout << " sum = " << sum << endl;
return;
}
// parent node save
path[level] = node->data;
pathFinder(node->left, path, level+1);
pathFinder(node->right, path, level+1);
}
struct Tree* insertNode(Tree *node, int data)
{
node->data = data;
node->left = NULL;
node->right = NULL;
return node;
}
int main(int argc, char **argv)
{
Tree *root = NULL;
Tree *nodeLeft = NULL;
Tree *nodeRight = NULL;
// unsorted binary tree
// root
root = insertNode(new Tree, 3);
// 1st level
nodeLeft = insertNode(new Tree, -1);
root->left = nodeLeft;
nodeRight = insertNode(new Tree, 2);
root->right = nodeRight;
// 2nd level
nodeLeft->left = insertNode(new Tree, 5);
nodeLeft->right = insertNode(new Tree, 7);
nodeRight->left = insertNode(new Tree, 1);
// path find
int path[10];
pathFinder(root,path,0);
return 0;
}
/* output */
/*
3 -1 5 sum = 7
3 -1 7 sum = 9
3 2 1 sum = 6
*/
The code below constructs binary search tree with minimal height for an int array which is already sorted in increasing order.
The middle element becomes a root and each sides of the mid element go to either left or right side of the tree. We do it recursively so that middle element always becomes the root for each subtree.
#include <iostream>
typedef struct node
{
node *left;
node *right;
int data;
} Node;
Node *btree(int a[], int low, int high)
{
if(low > high) return NULL;
int mid = (low + high) /2;
Node *nd = new Node;
nd->data = a[mid];
nd->left = btree(a, low, mid-1);
nd->right = btree(a, mid+1, high);
return nd;
}
int main()
{
int a[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
int size = sizeof(a)/sizeof(int);
Node *root = btree(a, 0, size-1);
return 0;
}
Is the two BST same?
The code below compares both structure and data and check if both are the same.
bool isTreeEqual (TREE*, TREE*) takes both of the nodes as its parameters. As soon as it detects the difference, it returns false, and returns true only after passing all the tests.
/* Compare two Binary Trees */
#include <iostream>
using namespace std;
typedef struct Tree
{
char data;
Tree *left;
Tree *right;
} TREE;
TREE* newTree(char ch)
{
TREE *node = new TREE;
node->data = ch;
node->left = NULL;
node->right = NULL;
return node;
}
void insertTreeNode(TREE *node, char ch)
{
TREE *newNode = new TREE;
newNode->data = ch;
newNode->left = NULL;
newNode->right = NULL;
while(node) {
if(ch <= node->data) {
if(node->left == NULL) {
node->left = newNode;
return;
}
else
node = node->left;
}
else {
if(node->right == NULL) {
node->right = newNode;
return;
}
else
node = node->right;
}
}
}
bool isTreeEqual(TREE* node1, TREE* node2)
{
// handles the roots are equal or both NULL
if(node1 == node2)
return true;
// one of them NULL
if(node1 == NULL || node2 == NULL)
return false;
// data check
if(node1->data != node2->data)
return false;
if(!isTreeEqual(node1->left, node2->left))
return false;
if(!isTreeEqual(node1->right, node2->right))
return false;
// everything has been checked, return true
return true;
}
void clear(TREE* node)
{
if(node != NULL) {
clear(node->left);
clear(node->right);
delete node;
}
}
int main(int argc, char **argv)
{
char charArr[]
= {'F','B','A','D','C','E','G','I','H'};
int size = sizeof(charArr)/sizeof(charArr[0]);
TREE *root1 = newTree('F');
for(int i = 1; i < size; i++)
insertTreeNode(root1,charArr[i]);
// same roots
cout << "isTreeEqual(root1, root1) = "
<< isTreeEqual(root1, root1) << endl;
TREE *root2 = newTree('F');
for(int i = 1; i < size; i++)
insertTreeNode(root2,charArr[i]);
// same structure & data
cout << "isTreeEqual(root1, root2) = "
<< isTreeEqual(root1, root2) << endl;
// same structure but the last leaf is different
char charArr3[]
= {'F','B','A','D','C','E','G','I','Z'};
TREE *root3 = newTree('F');
for(int i = 1; i < size; i++)
insertTreeNode(root3,charArr3[i]);
cout << "isTreeEqual(root1, root3) = "
<< isTreeEqual(root1, root3) << endl;
// root4 has one more leaf node 'J'
char charArr4[]
= {'F','B','A','D','C','E','G','I','H','J'};
size = sizeof(charArr4)/sizeof(charArr4[0]);
TREE *root4 = newTree('F');
for(int i = 1; i < size; i++)
insertTreeNode(root4,charArr4[i]);
cout << "isTreeEqual(root1, root4) = "
<< isTreeEqual(root1, root4) << endl;
// root = NULL
cout << "isTreeEqual(root1, 0) = "
<< isTreeEqual(root1, 0) << endl;
// both roots are NULL
cout << "isTreeEqual(0, 0) = "
<< isTreeEqual(0, 0) << endl;
// deallocate
clear(root1);
clear(root2);
clear(root3);
clear(root4);
return 0;
}
Output:
isTreeEqual(root1, root1) = 1 isTreeEqual(root1, root2) = 1 isTreeEqual(root1, root3) = 0 isTreeEqual(root1, root4) = 0 isTreeEqual(root1, 0) = 0 isTreeEqual(0, 0) = 1
Deleting a key from a binary search is a little bit tricky. We can categorize it in three groups depending its operations:
The colde below is based on the BST in the picture.

/* Binary Tree - deleting a node*/
#include <iostream>
using namespace std;
typedef struct Tree
{
char data;
Tree *left;
Tree *right;
Tree *parent;
} TREE;
TREE *newTreeNode(int data)
{
TREE *node = new TREE;
node->data = data;
node->left = NULL;
node->right = NULL;
node->parent = NULL;
return node;
}
void insertTreeNode(TREE *node, char ch)
{
TREE *newNode = new TREE;
newNode->data = ch;
newNode->left = NULL;
newNode->right = NULL;
while(node) {
if(ch <= node->data) {
if(node->left == NULL) {
newNode->parent = node;
node->left = newNode;
return;
}
else
node = node->left;
}
else {
if(node->right == NULL) {
newNode->parent = node;
node->right = newNode;
return;
}
else
node = node->right;
}
}
}
TREE *getNode(TREE *node, char c)
{
if(node == NULL) return node;
if(c < node->data)
return getNode(node->left,c);
else if( c > node->data)
return getNode(node->right, c);
else
return node;
}
char treeMax(TREE *node)
{
while(node->right) {
node = node->right;
}
return node->data;
}
void printTreeInOrder(TREE *node)
{
if(node == NULL) return;
printTreeInOrder(node->left);
cout << node->data << " ";
printTreeInOrder(node->right);
}
char predecessorInOrder(TREE *node)
{
if(node->left)
return treeMax(node->left);
TREE *y = node->parent;
while(node == y->left) {
node = y;
y = y->parent;
}
return y->data;
}
void deleteKey(TREE *root, char ch)
{
TREE *node, *p, *child, *pred;
// get the node for the key
node = getNode(root, ch);
// leaf node - just delete the node
if(node->left == NULL && node->right == NULL) {
if(node->parent) p = node->parent;
if(node == p->left)
p->left = NULL;
else
p->right = NULL;
delete node;
return;
}
// two children - replace it with its predecessor and delete
if(node->left && node->right) {
char ch_pred = predecessorInOrder(node);
pred = getNode(root, ch_pred);
if(pred->parent->left == pred)
pred->parent->left = NULL;
else if(pred->parent->right == pred)
pred->parent->right = NULL;
node->data = pred->data;
delete pred;
return;
}
// only one child
// replace it with its child and delete
if(node->left)
child = node->left;
else if(node->right)
child = node->right;
p = node->parent;
if(p->left && p->left == node) {
p->left = child;
}
else if (p->right && p->right == node) {
p->right = child;
}
child->parent = p;
delete node;
return;
}
int main(int argc, char **argv)
{
TREE *root = newTreeNode('F');
insertTreeNode(root,'B');
insertTreeNode(root,'A');
insertTreeNode(root,'D');
insertTreeNode(root,'C');
insertTreeNode(root,'E');
insertTreeNode(root,'G');
insertTreeNode(root,'I');
insertTreeNode(root,'H');
printTreeInOrder(root);
cout << "\ndeleteKey(root, 'A')" << endl;
deleteKey(root, 'A');
printTreeInOrder(root);
cout << "\ninsertTreeNode(root,'A')" << endl;
insertTreeNode(root,'A');
printTreeInOrder(root);
cout << "\ndeleteKey(root, 'I')" << endl;
deleteKey(root, 'I');
cout << "deleteKey(root, 'H')" << endl;
deleteKey(root, 'H');
printTreeInOrder(root);
cout << "\ninsertTreeNode(root,'I')" << endl;
insertTreeNode(root,'I');
cout << "insertTreeNode(root,'H')" << endl;
insertTreeNode(root,'H');
printTreeInOrder(root);
cout << "\ndeleteKey(root, 'F') " << endl;
deleteKey(root, 'F');
printTreeInOrder(root);
return 0;
}
Output is:
A B C D E F G H I deleteKey(root, 'A') B C D E F G H I insertTreeNode(root,'A') A B C D E F G H I deleteKey(root, 'I') deleteKey(root, 'H') A B C D E F G insertTreeNode(root,'I') insertTreeNode(root,'H') A B C D E F G H I deleteKey(root, 'F') A B C D E G H I
No algorithm that sort by comparison based can do beter than $n \log n$ performance in the average or worst case.
Given $n$ items, there are ${n!}$ permutations of these elements. Each internal node of binary decision tree represents a comparison $a_i \le a_j$ and the leaves of the tree represents on of ${n!}$. Though there are numerous constructs for binary decision tree, we can compute its minimum height, $h$. In other words, there must be some leaf that requires $h$ comparison nodes in the tree from the root to that leaf.
Let's assume we have complete binary tree of height $h$ in which all non-leaf nodes have both a left and a right child. This tree contains $n=2^h-1$ nodes. The height will be $h = \log (n+1)$. Any binary decision tree with ${n!}$ leaf nodes has at least ${n!}$ nodes. So, we need to compute $h=[\log({n!})]$ to determine the height of the binary decision tree.
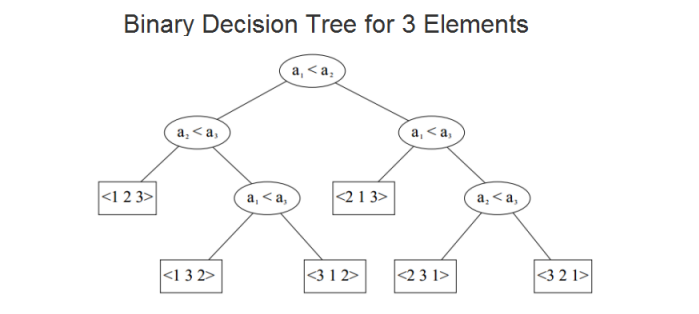
$$\begin{align} h & \ge \log({n!}) \\ & = \log(n(n-1)(n-2)...(2)(1)) \\ & = \log(n) + \log(n-1) + \log(n-2) + ...+ \log 2 +\log 1 \\ & = \sum_{i={n/2}}^n \log i + \sum_{i=1}^{n/2-1} \log i \\ & \ge \sum_{i={n/2}}^n \log i \\ & \ge \sum_{i={n/2}}^n \log {n \over 2} \\ & = {n \over 2} \log {n \over 2} \\ & = \Omega (n \log n) \end{align}$$
So, any sorting algorithm using comparisons will require $\Omega(n \log n)$ comparisons to sort.
An alternative sorting algorithm such as bucket sort would perform better under specific conditions. That's because it is not solely rely on comparing elements.
Bogotobogo Image / Video Processing
Computer Vision & Machine Learning
with OpenCV, MATLAB, FFmpeg, and scikit-learn.
Bogotobogo's Video Streaming Technology
with FFmpeg, HLS, MPEG-DASH, H.265 (HEVC)
Bogotobogo's contents
To see more items, click left or right arrow.
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization
























































































































