scikit-learn : Radial Basis Function kernel, RBF

"In Euclidean geometry linearly separable is a geometric property of a pair of sets of points. This is most easily visualized in two dimensions (the Euclidean plane) by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are linearly separable if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher dimensional Euclidean spaces if line is replaced by hyperplane." - wiki : Linear separability
"Some supervised learning problems can be solved by very simple models (called generalized linear models) depending on the data. Others simply don't." - Machine Learning 101 - General Concepts
For better understanding, we'll run svm_gui.py which is under sklearn_tutorial/examples directory. We can download the tutorial from Tutorial Setup and Installation:
git clone https://github.com/astroML/sklearn_tutorial
It's an interactive example.
$ python $SKL_HOME/examples/svm_gui.py
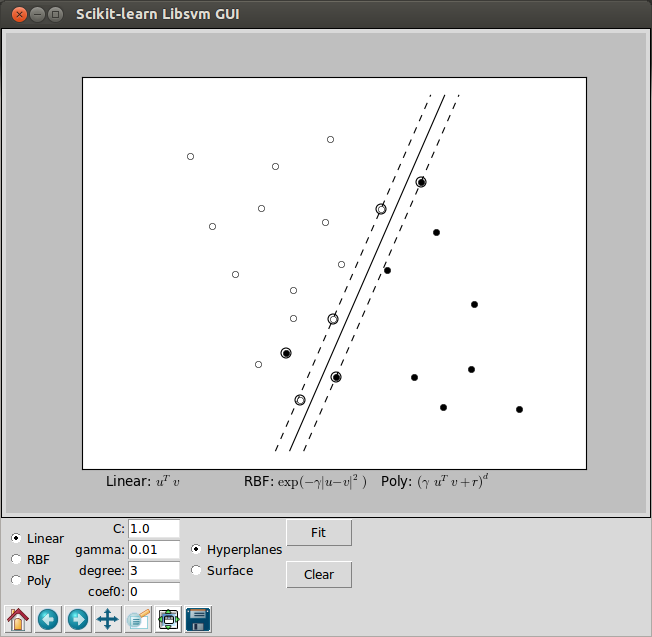
Accuracy: 95.8333333333:
Accuracy: 66.6666666667:
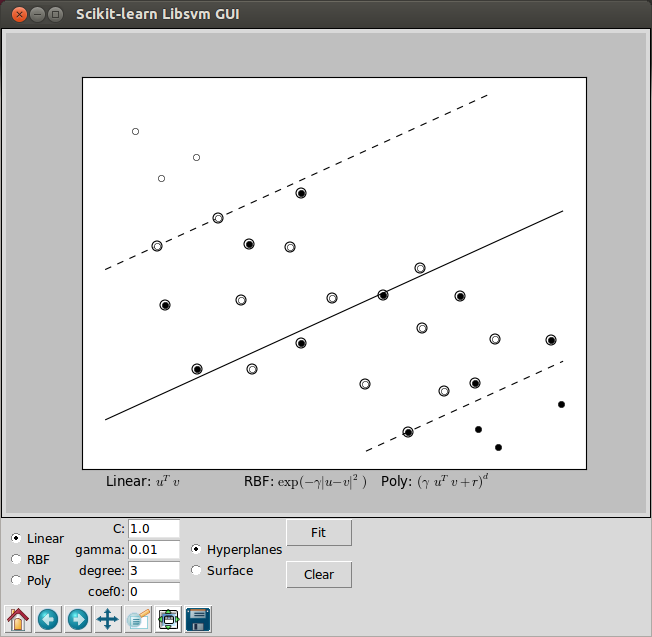
The two pictures above used the Linear Support Vector Machine (SVM) that has been trained to perfectly separate 2 sets of data points labeled as white and black in a 2D space. Note that we used hyperplane as a separator
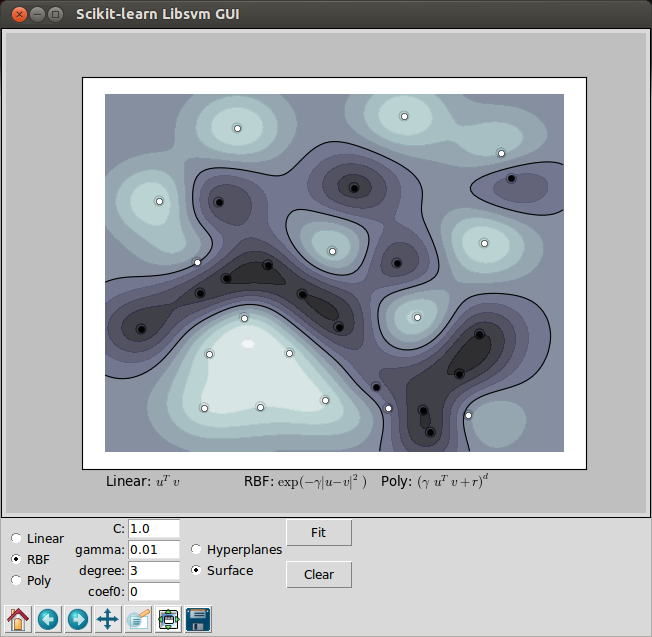
SVM with gaussian RBF (Radial Gasis Function) kernel is trained to separate 2 sets of data points. The points are labeled as white and black in a 2D space. This dataset cannot be separated by a simple linear model.
However, as we can see from the picture below, they can be easily kernelized to solve nonlinear classification, and that's one of the reasons why SVMs enjoy high popularity.
"In machine learning, the (Gaussian) radial basis function kernel, or RBF kernel, is a popular kernel function used in support vector machine classification." - Radial basis function kernel
Let's see how a nonlinear classification problem looks like using a sample dataset created by XOR logical operation (outputs true only when inputs differ - one is true, the other is false).
In the code below, we create XOR gate dataset (500 samples with either a class label of 1 or -1) using NumPy's logical_xor function:
import numpy as np import matplotlib.pyplot as plt np.random.seed(0) X_xor = np.random.randn(1000, 2) y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] > 0) y_xor = np.where(y_xor, 1, -1) plt.scatter(X_xor[y_xor==1, 0], X_xor[y_xor==1, 1], c='b', marker='x', label='1') plt.scatter(X_xor[y_xor==-1, 0], X_xor[y_xor==-1, 1], c='r', marker='s', label='-1') plt.ylim(-3.0) plt.legend() plt.show()
Here is the plot:
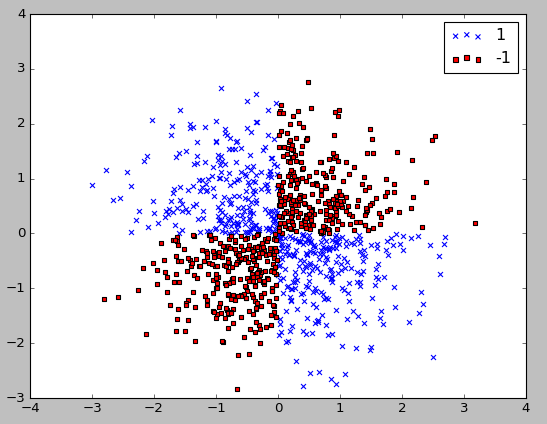
As we can see from the plot, we cannot separate samples using a linear hyperplane as the decision boundary via linear SVM model or logistic regression.
The kernel methods is to deal with such a linearly inseparable data is to create nonlinear combinations of the original features to project the dataset onto a higher dimensional space via a mapping function and make them linearly separable.
As shown in the picture below, we can transform a two-dimensional dataset onto a new three-dimensional feature space where the classes become separable via the following projection:
$$\phi(x_1, x_2) = (z_1, z_2, z_3) = (x_1, x_2, x_1^2+x_2^2)$$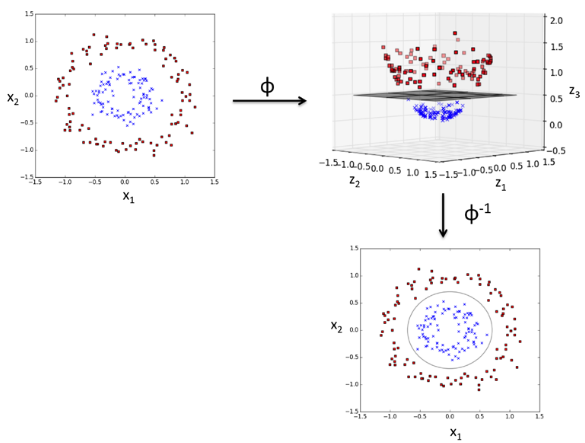
Picture credit : Python Machine Learning by Sebastian Raschka
The solution by a non-linear kernel is available SVM II - SVM with nonlinear decision boundary for xor dataset.
Machine Learning with scikit-learn
scikit-learn installation
scikit-learn : Features and feature extraction - iris dataset
scikit-learn : Machine Learning Quick Preview
scikit-learn : Data Preprocessing I - Missing / Categorical data
scikit-learn : Data Preprocessing II - Partitioning a dataset / Feature scaling / Feature Selection / Regularization
scikit-learn : Data Preprocessing III - Dimensionality reduction vis Sequential feature selection / Assessing feature importance via random forests
Data Compression via Dimensionality Reduction I - Principal component analysis (PCA)
scikit-learn : Data Compression via Dimensionality Reduction II - Linear Discriminant Analysis (LDA)
scikit-learn : Data Compression via Dimensionality Reduction III - Nonlinear mappings via kernel principal component (KPCA) analysis
scikit-learn : Logistic Regression, Overfitting & regularization
scikit-learn : Supervised Learning & Unsupervised Learning - e.g. Unsupervised PCA dimensionality reduction with iris dataset
scikit-learn : Unsupervised_Learning - KMeans clustering with iris dataset
scikit-learn : Linearly Separable Data - Linear Model & (Gaussian) radial basis function kernel (RBF kernel)
scikit-learn : Decision Tree Learning I - Entropy, Gini, and Information Gain
scikit-learn : Decision Tree Learning II - Constructing the Decision Tree
scikit-learn : Random Decision Forests Classification
scikit-learn : Support Vector Machines (SVM)
scikit-learn : Support Vector Machines (SVM) II
Flask with Embedded Machine Learning I : Serializing with pickle and DB setup
Flask with Embedded Machine Learning II : Basic Flask App
Flask with Embedded Machine Learning III : Embedding Classifier
Flask with Embedded Machine Learning IV : Deploy
Flask with Embedded Machine Learning V : Updating the classifier
scikit-learn : Sample of a spam comment filter using SVM - classifying a good one or a bad one
Machine learning algorithms and concepts
Batch gradient descent algorithmSingle Layer Neural Network - Perceptron model on the Iris dataset using Heaviside step activation function
Batch gradient descent versus stochastic gradient descent
Single Layer Neural Network - Adaptive Linear Neuron using linear (identity) activation function with batch gradient descent method
Single Layer Neural Network : Adaptive Linear Neuron using linear (identity) activation function with stochastic gradient descent (SGD)
Logistic Regression
VC (Vapnik-Chervonenkis) Dimension and Shatter
Bias-variance tradeoff
Maximum Likelihood Estimation (MLE)
Neural Networks with backpropagation for XOR using one hidden layer
minHash
tf-idf weight
Natural Language Processing (NLP): Sentiment Analysis I (IMDb & bag-of-words)
Natural Language Processing (NLP): Sentiment Analysis II (tokenization, stemming, and stop words)
Natural Language Processing (NLP): Sentiment Analysis III (training & cross validation)
Natural Language Processing (NLP): Sentiment Analysis IV (out-of-core)
Locality-Sensitive Hashing (LSH) using Cosine Distance (Cosine Similarity)
Artificial Neural Networks (ANN)
[Note] Sources are available at Github - Jupyter notebook files1. Introduction
2. Forward Propagation
3. Gradient Descent
4. Backpropagation of Errors
5. Checking gradient
6. Training via BFGS
7. Overfitting & Regularization
8. Deep Learning I : Image Recognition (Image uploading)
9. Deep Learning II : Image Recognition (Image classification)
10 - Deep Learning III : Deep Learning III : Theano, TensorFlow, and Keras
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization